

Next: Data interpolation
Up: Multiple linear regression as
Previous: Introduction
The method of multiple linear regression (MLR) is based on the
assumption that every measured parameter 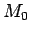 can be expressed in
the form of linear combination of other parameter
can be expressed in
the form of linear combination of other parameter 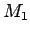 ,
,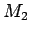 ,...
,...
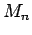 in the form:
in the form:
Using MLR the unknown a's in such a formula can be calculated from at
least n different sets of measurements of 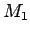 to
to 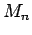 .
.
This assumption can easily be related to the mixing of water masses.
Lets take 3 water masses 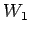 ,
,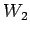 and
and 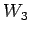 each with its
characteristic parameter value
each with its
characteristic parameter value
 ,
,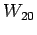 ,
,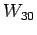 for parameter
for parameter 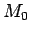 ;
;
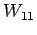 ,
,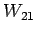 ,
,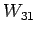 for parameter
for parameter 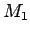 ; etc..
The result of mixing these water masses is expressed in following form:
; etc..
The result of mixing these water masses is expressed in following form:
with 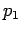 ,
,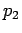 ,
,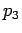 being the percentage of the respectively
watermasses 1,2 and 3 in the mixture, and the last equation
expressing mass conservation. If the water mass percentages
being the percentage of the respectively
watermasses 1,2 and 3 in the mixture, and the last equation
expressing mass conservation. If the water mass percentages 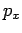 and
the parameter
and
the parameter 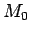 are not known, we can calculate
are not known, we can calculate 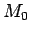 using the
last 3 formulas arriving at:
using the
last 3 formulas arriving at:
where 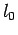 ,
,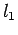 and
and  are lengthy formulas involving only the
are lengthy formulas involving only the
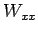 's. If also the
's. If also the 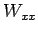 's are not known it is possible to
use other measured bottle data; bottle
's are not known it is possible to
use other measured bottle data; bottle 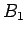 with measured parameters
with measured parameters
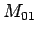 ,
,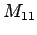 ,
,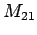 ; bottle
; bottle 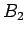 with
with
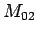 ,
,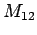 ,
,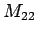 ; etc., to determine the unknown l's. A
minimum of 3 different bottles are then necessary to calculate
; etc., to determine the unknown l's. A
minimum of 3 different bottles are then necessary to calculate
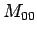 (the unknown
(the unknown 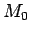 from bottle 0) and a minimum of 9 would
be necessary to calculate all the
from bottle 0) and a minimum of 9 would
be necessary to calculate all the 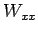 's. If the mixing implies
more watermasses we always need at least the same amount of
parameters M and bottles B as there are different water masses.
's. If the mixing implies
more watermasses we always need at least the same amount of
parameters M and bottles B as there are different water masses.
If the parameter 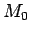 is not only passively mixed but has also
sources and sinks which are related linearly to a parameter
is not only passively mixed but has also
sources and sinks which are related linearly to a parameter 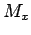 (like the nitrate source is related linearly to the apparent oxygen
utilization by the redfield ratio) we can just add this term to the
formula for
(like the nitrate source is related linearly to the apparent oxygen
utilization by the redfield ratio) we can just add this term to the
formula for 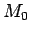 :
:
and
use the same MLR to calculate 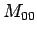 .
.
Other processes that can have an effect on 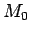 are not correlated
in a linear way to some parameter
are not correlated
in a linear way to some parameter 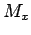 , as there are radioactive
decay, solubility, etc., or the redfield ratio from the last formula
is not constant, which can result in a locally varying factor k. But
if only deviations from a fixed reference are considered, we can
linearize these processes within a small error margin and once again
use the MLR. One way to consider only small deviations is to use
only bottles in the proximity of bottle 0 where
, as there are radioactive
decay, solubility, etc., or the redfield ratio from the last formula
is not constant, which can result in a locally varying factor k. But
if only deviations from a fixed reference are considered, we can
linearize these processes within a small error margin and once again
use the MLR. One way to consider only small deviations is to use
only bottles in the proximity of bottle 0 where 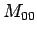 is to be
calculated. A positive side-effect of this more local approach is
that fewer watermasses have to be considered in the calculation.
is to be
calculated. A positive side-effect of this more local approach is
that fewer watermasses have to be considered in the calculation.
In the following we are giving an incomplete list of parameter
correlations, not necessary linear ones, which are not due to mixing
or due to the equation of state.
- Nitrate (NO
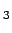 ) - Phosphate (PO
) - Phosphate (PO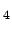 ) - dissolved inorganic
carbon (T-C) - apparent
oxygen utilization (AOU) due to the constant redfield ration and the
processes of formation and remineralization of organic material
) - dissolved inorganic
carbon (T-C) - apparent
oxygen utilization (AOU) due to the constant redfield ration and the
processes of formation and remineralization of organic material
- potential temperature (
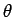 ) with gases like CO
) with gases like CO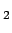 ,
oxygen, etc. due to the temperature dependency of the solubility
,
oxygen, etc. due to the temperature dependency of the solubility
- in the Atlantic silica (SiO
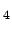 ) correlates with the percentage
of water of southern (or pacific) origin .
) correlates with the percentage
of water of southern (or pacific) origin .
- a pacific origin of water masses is again correlated with
higher alkalinity and terrigenic helium.
- apparent oxygen utilization is correlated with age if we can
assume a constant respiration ratio
- age again correlates with anthropogenic tracers like tritium,
freon or CCl
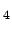


Next: Data interpolation
Up: Multiple linear regression as
Previous: Introduction
Juergen Holfort
2004-08-12
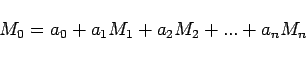
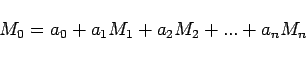
![]() ,
,![]() and
and ![]() each with its
characteristic parameter value
each with its
characteristic parameter value
![]() ,
,![]() ,
,![]() for parameter
for parameter ![]() ;
;
![]() ,
,![]() ,
,![]() for parameter
for parameter ![]() ; etc..
The result of mixing these water masses is expressed in following form:
; etc..
The result of mixing these water masses is expressed in following form:
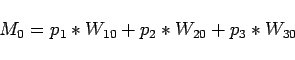
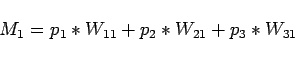

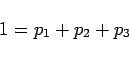

![]() is not only passively mixed but has also
sources and sinks which are related linearly to a parameter
is not only passively mixed but has also
sources and sinks which are related linearly to a parameter ![]() (like the nitrate source is related linearly to the apparent oxygen
utilization by the redfield ratio) we can just add this term to the
formula for
(like the nitrate source is related linearly to the apparent oxygen
utilization by the redfield ratio) we can just add this term to the
formula for ![]() :
: 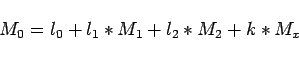
![]() are not correlated
in a linear way to some parameter
are not correlated
in a linear way to some parameter ![]() , as there are radioactive
decay, solubility, etc., or the redfield ratio from the last formula
is not constant, which can result in a locally varying factor k. But
if only deviations from a fixed reference are considered, we can
linearize these processes within a small error margin and once again
use the MLR. One way to consider only small deviations is to use
only bottles in the proximity of bottle 0 where
, as there are radioactive
decay, solubility, etc., or the redfield ratio from the last formula
is not constant, which can result in a locally varying factor k. But
if only deviations from a fixed reference are considered, we can
linearize these processes within a small error margin and once again
use the MLR. One way to consider only small deviations is to use
only bottles in the proximity of bottle 0 where ![]() is to be
calculated. A positive side-effect of this more local approach is
that fewer watermasses have to be considered in the calculation.
is to be
calculated. A positive side-effect of this more local approach is
that fewer watermasses have to be considered in the calculation.